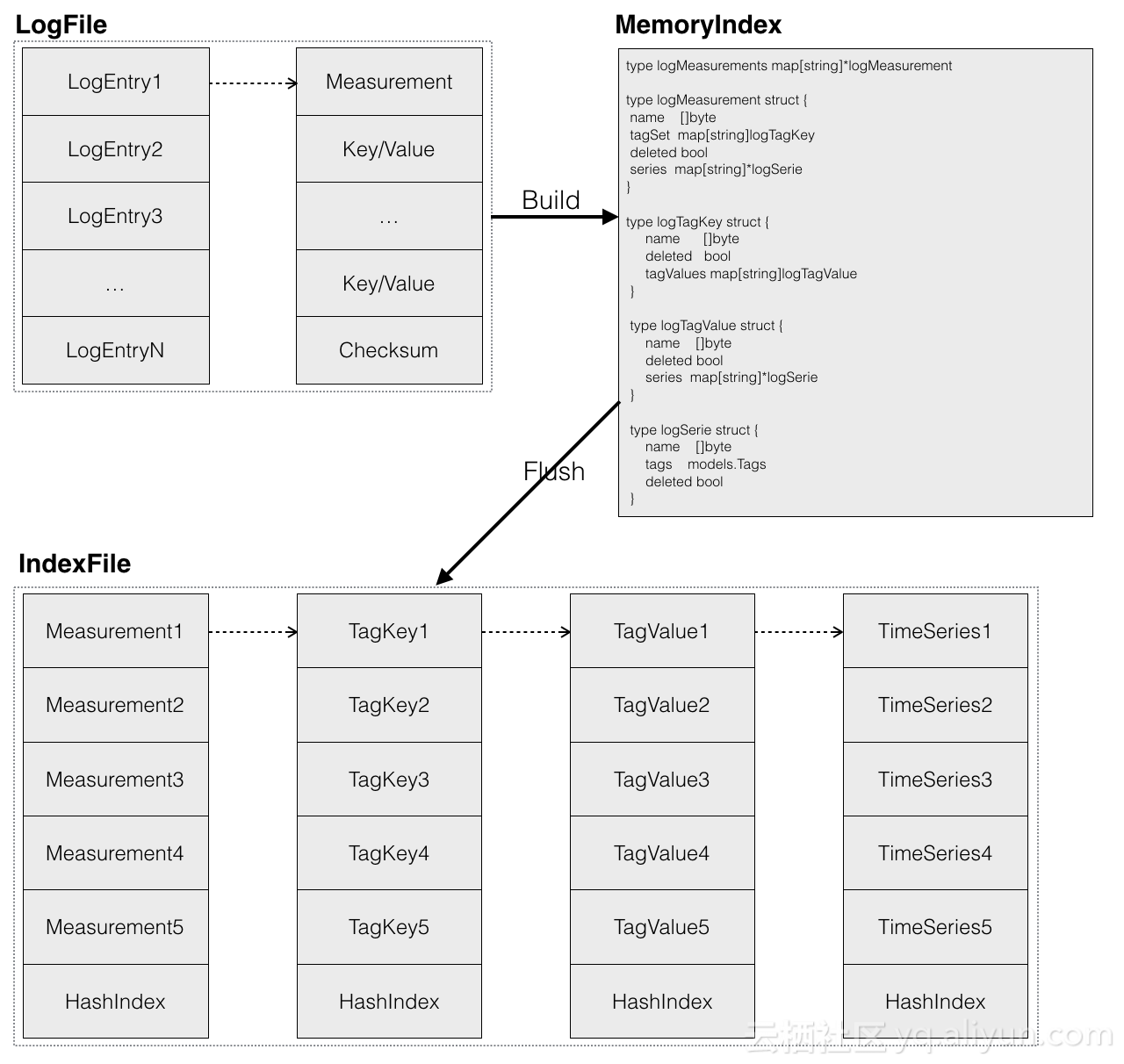
介绍

本文主要介绍一些二叉树结构，代码语言为 golang，地址:

二叉树

二叉树（Binary Tree）是包含 n 个节点的有限集合，该集合或者为空集（此时，二叉树称为空树），或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。

二叉查找树

满足左大右小即可，是一种非常简单的二叉树

1. 插入使用递归，从上到下查找新节点在树种的合适位置
2. 删除时候需分以下三种情况进行考虑:
   

AVL 树

AVL 树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的”AVL 旋转”。

1. 插入
   以下图表以四列表示四种情况，每行表示在该种情况下要进行的操作。在左左和右右的情况下，只需要进行一次旋转操作；在左右和右左的情况下，需要进行两次旋转操作。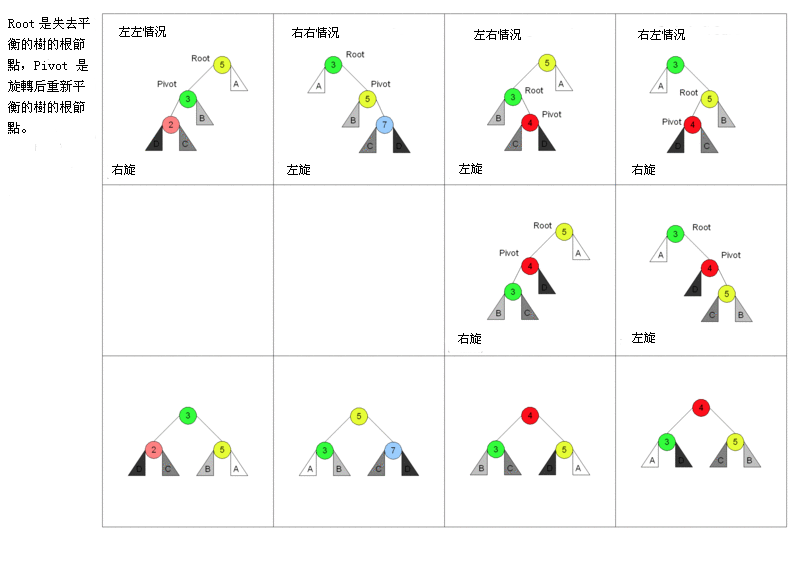
   

2. 删除
   从 AVL 树中删除，可以通过把要删除的节点向下旋转成一个叶子节点，接着直接移除这个叶子节点来完成。因为在旋转成叶子节点期间最多有 log n 个节点被旋转，而每次 AVL 旋转耗费固定的时间，所以删除处理在整体上耗费 O(log n) 时间。

3. 搜索
   可以像普通二叉查找树一样的进行，所以耗费 O(log n)时间，因为 AVL 树总是保持平衡的。不需要特殊的准备，树的结构不会由于查找而改变。（这是与伸展树搜索相对立的，它会因为搜索而变更树结构。）

红黑树

B 树

B+树

B*树

Trie 树

HAT-Trie

前缀树

Generalized Prefix Tree (GPT)

后缀树

Succinct Trie

基数(Radix)树

对于长整型数据的映射，如何解决 Hash 冲突和 Hash 表大小的设计是一个很头疼的问题。
radix 树就是针对这种稀疏的长整型数据查找，能快速且节省空间地完成映射。借助于 Radix 树，我们可以实现对于长整型数据类型的路由。利用 radix 树可以根据一个长整型（比如一个长 ID）快速查找到其对应的对象指针。这比用 hash 映射来的简单，也更节省空间，使用 hash 映射 hash 函数难以设计，不恰当的 hash 函数可能增大冲突，或浪费空间。

radix tree 是一种多叉搜索树，树的叶子结点是实际的数据条目。每个结点有一个固定的、2^n 指针指向子结点（每个指针称为槽 slot，n 为划分的基的大小）

radix Tree(基数树) 其实就差不多是传统的二叉树，只是在寻找方式上，利用比如一个 unsigned int 的类型的每一个比特位作为树节点的判断。
可以这样说，比如一个数 1000101010101010010101010010101010，那么按照 Radix 树的插入就是在根节点，如果遇到 0，就指向左节点，如果遇到 1 就指向右节点，在插入过程中构造树节点，在删除过程中删除树节点。如果觉得太多的调用 Malloc 的话，可以采用池化技术，预先分配多个节点。
（使用一个比特位判断，会使树的高度过高，非叶节点过多。故在实际应用中，我们一般是使用多个比特位作为树节点的判断，但多比特位会使节点的子节点槽变多，增大节点的体积，一般选用 2 个或 4 个比特位作为树节点即可）

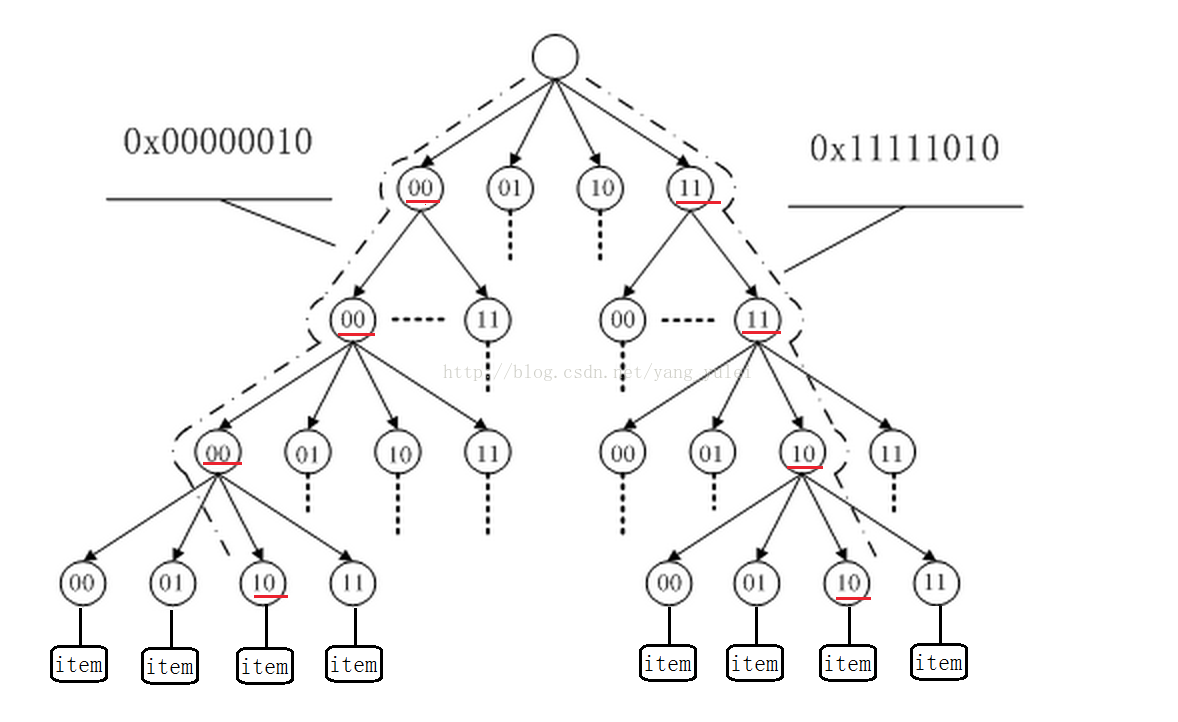
Radix 树在 Linux 中的应用：

Linux 基数树（radix tree）是将 long 整数键值与指针相关联的机制，它存储有效率，并且可快速查询，用于整数值与指针的映射（如：IDR 机制）、内存管理等。
IDR（ID Radix）机制是将对象的身份鉴别号整数值 ID 与对象指针建立关联表，完成从 ID 与指针之间的相互转换。IDR 机制使用 radix 树状结构作为由 id 进行索引获取指针的稀疏数组，通过使用位图可以快速分配新的 ID，IDR 机制避免了使用固定尺寸的数组存放指针。IDR 机制的 API 函数在 lib/idr.c 中实现。

Linux radix 树最广泛的用途是用于 内存管理，结构 address_space 通过 radix 树 跟踪绑定到地址映射上的核心页，该 radix 树允许内存管理代码快速查找标识为 dirty 或 writeback 的页。其使用的是数据类型 unsigned long 的固定长度输入的版本。每级代表了输入空间固定位数。Linux radix 树的 API 函数在 lib/radix-tree.c 中实现。（把页指针和描述页状态的结构映射起来，使能快速查询一个页的信息。）

Linux 内核利用 radix 树在文件内偏移快速定位文件缓存页。
Linux(2.6.7) 内核中的分叉为 64(2^6)，树高为 6(64 位系统)或者 11(32 位系统)，用来快速定位 32 位或者 64 位偏移，radix tree 中的每一个叶子节点指向文件内相应偏移所对应的 Cache 项。

radix 树为稀疏树提供了有效的存储，代替固定尺寸数组提供了键值到指针的快速查找。

Radix 树与 Trie 树的思想有点类似，甚至可以把 Trie 树看为一个基为 26 的 Radix 树。（也可以把 Radix 树看做是 Tire 树的变异）
Trie 树一般用于字符串到对象的映射，Radix 树一般用于长整数到对象的映射。
trie 树主要问题是树的层高，如果要索引的字的拼音很长很变态，我们也要建一个很高很变态的树么？
radix 树能固定层高（对于较长的字符串，可以用数学公式计算出其特征值，再用 radix 树存储这些特征值）

1. 插入
   我们在插入一个新节点时，我们根据数据的比特位，在树中向下查找，若没有相应结点，则生成相应结点，直到数据的比特位访问完，则建立叶节点映射相应的对象。

2. 删除
   我们可以“惰性删除”，即沿着路径查找到叶节点后，直接删除叶节点，中间的非叶节点不删除。

ART 树

KISS 树

FAST 树

1. pointer-free
2. no online
3. k-ary
4. GPU implementation

T 树

R 树

R+树

R*树

QR 树

SS 树

X 树

参考文献

1. [Data Structure] 数据结构中各种树 http://www.cnblogs.com/maybe2030/p/4732377.html
2. ARThttps://db.in.tum.de/~leis/papers/ART.pdf
3. 内存数据库中的索引技术https://blog.csdn.net/zhujunxxxxx/article/details/42490335

原文链接： Time Series Index (TSI) details

Time Series Index (TSI) description

当 InfluxDB 插入数据时，不仅需要存储 value 同时也需要为 measurement 和 tag 等做索引来加快查询速度。在之前的版本中，索引数据只存在内存中，这就要求大量的 RAM 并且需要设置机器所能承受的序列容量的上限，根据所用机器的不同，通常这个上限在 100-400 万之间。

时间序列索引（TSI）的设计就是为了超过容量上限。TSI 将索引存储在磁盘上，所以可以不再收到 RAM 的限制。TSI 使用操作系统的页面缓存将热数据提取到内存中，让冷数据驻留在磁盘上。

目前 TSM 和查询引擎中存在着一些限制。制约了一个节点所能存放的时间序列的数量。实际的存储上限通常为 3000 万左右。

Tooling

influx_inspect dumptsi

如果要解决索引问题，可以使用 Influx_inspect dumptsi 命令。此命令允许您打印索引、文件或一组文件的摘要统计信息。此命令一次仅适用于一个索引。
有关此命令的详细信息，请参阅 Influx_inspect dumptsi。

influx_inspect buildtsi

如果要将现有分片从内存中索引转换为 TSI 索引，或者如果现有 TSI 索引已损坏，则可以使用buildtsi命令从基础 TSM 数据创建索引。如果您要重建现有 TSI 索引，请首先删除分片中的index目录。

此命令在服务器级别工作，但您可以选择添加数据库，保留策略和分片筛选器以仅应用于分片子集。

有关此命令的详细信息，请参阅Influx inspect buildtsi

Understanding TSI

File organization

TSI（时间序列索引）基于日志合并树(LSMT)，用于 InfluxDB 中存储时间序列。 TSI 由几个部分组成：

• Index：包含单个分片(shard)的整个索引数据集。
• Partition：包含分片数据的分片分区。
• LogFile：包含新写入序列并作为内存索引，并作为 WAL 保留。
• IndexFile：包含从单个 LogFile 构建或从两个连续索引文件合并的不可变内存映射索引。

还有一个 SeriesFile，它包含整个数据库中所有序列的 keys 的集合。数据库中的每个分片共享相同的 series 文件。

Writes

写入到来时会发生以下情况：

• 将该 Series 添加到 Series 文件中，如果已存在则查找。返回一个自动递增 Series ID。
• 将该 Series 加到索引中。索引维护现有 Series IDs 的 roaring bitmap，并忽略已创建的 Series。
• 该 Series 经过哈希处理后添加进相应的分区。
• 分区将该 Series 写为 LogFile 上的一条记录。
• LogFile 将该 Series 写到磁盘上的预写日志文件（WAL），并将该 Series 添加到内存索引中。

Compaction

一旦 LogFile 超过阈值（5MB），就会创建一个新的活动日志文件，并且前一个文件开始压缩到 IndexFile 中。第一个索引文件位于 1 级（L1）。日志文件被视为级别 0（L0）。

也可以通过将两个较小的索引文件合并在一起来创建索引文件。例如，如果存在连续的两个 L1 索引文件，则它们可以合并到 L2 索引文件中。

Reads

该索引提供了几个用于检索数据集的 API 调用，例如：

• MeasurementIterator()：返回 measurement names 的排序列表。
• TagKeyIterator()：返回 measurement 中 tag keys 的排序列表。
• TagValueIterator()：返回一个 tag key 的 tag values 的排序列表。
• MeasurementSeriesIDIterator()：返回 measurement 的所有 series ID 的排序列表。
• TagKeySeriesIDIterator()：返回 一个 tag key 的所有 series ID 的排序列表。
• TagValueSeriesIDIterator()：返回 一个 tag value 所有 series ID 的排序列表。

这些迭代器都可以使用多个合并迭代器进行组合。对于每种类型的迭代器（measurement, tag key, tag value, series id），有多个合并迭代器类型：

• 合并：对两个迭代器中的项进行重复数据删除。
• 相交：仅返回两个迭代器中同时存在的项。
• 不同：仅返回在第一个迭代器中存在，在第二个迭代器中不存在的项。

例如，诸如跨两个分片的 WHERE 子句的查询 region != 'us-west',该构造一组类似如下的迭代器:

1
2
3
4
5
6
7
8
9
10

DifferenceSeriesIDIterators(
    MergeSeriesIDIterators(
        Shard1.MeasurementSeriesIDIterator("m"),
        Shard2.MeasurementSeriesIDIterator("m"),
    ),
    MergeSeriesIDIterators(
        Shard1.TagValueSeriesIDIterator("m", "region", "us-west"),
        Shard2.TagValueSeriesIDIterator("m", "region", "us-west"),
    ),
)

Log File Structure

日志文件简单地构造为按顺序写入磁盘的 LogEntry 对象列表。一旦达到 5MB 则写入日志文件，然后将它们压缩为索引文件。日志中的条目对象可以是以下任何类型：

• AddSeries
• DeleteSeries
• DeleteMeasurement
• DeleteTagKey
• DeleteTagValue

日志文件中的内存索引内容如下

• name 对应多个 measurement
• measurement 对应多个 tag key
• tag key 对应多个 tag value
• measurement 对应多个 Series
• tag value 对应多个 Series
• 用于 series, measurements, tag keys, and tag values 的删除标记(Tombstones)

日志文件还维护用于表示 Series ID 存在和删除的 bitsets。这些 bitsets 与其他日志文件和索引文件合并，以在启动时重新生成完整的 index bitset。

Index File Structure

索引文件是一个不可变的文件，它跟踪与日志文件类似的信息，但所有数据都被索引并写入磁盘，以便可以从内存映射中直接访问它。

索引文件包含以下部分：

• TagBlocks：维护一个索引，用于存放一个 tag key 的多个 tag values。
• MeasurementBlock：维护一个索引用于 measurements 和他们的 tag keys。
• Trailer：存储文件的偏移信息以及用于基数估计的 HyperLogLog skecthes。

Manifest

MANIFEST文件存储在索引目录中，列出了属于索引的所有文件以及它们应被访问的顺序。每次发生压缩时都会更新此文件。任何没有在文件夹下面的索引文件都是正在压缩的索引文件

FileSet

文件集是在 InfluxDB 进程运行时获取的清单的内存快照。这是提供某个时间点一致性索引视图所必需的。该文件集还便于对其所有文件进行引用计数，这样在文件的所有 readers 完成之前，不会通过压缩删除任何文件。

InfluxDB

InfluxDB 在 DB-Engines 的时序数据库类别里排名第一，实至名归，从它的功能丰富性、易用性以及底层实现来看，都有很多的亮点，值得大篇幅来分析。

首先简单归纳下它的几个比较重要的特性：

1. 极简架构：单机版的 InfluxDB 只需要安装一个 binary，即可运行使用，完全没有任何的外部依赖。相比来看几个反面例子，OpenTSDB 底层是 HBase，拖家带口就得带上 ZooKeeper、HDFS 等，如果你不熟悉 Hadoop 技术栈，一般运维起来是有一定的难度，这也是其被人抱怨最多的一个点。KairosDB 稍微好点，它依赖 Cassandra 和 ZooKeeper，单机测试可以使用 H2。总的来说，依赖一个外部的分布式数据库的 TSDB，在架构上会比完全自包含的 TSDB 复杂一点，毕竟一个成熟的分布式数据库本身就很复杂，当然这一点在云计算这个时代已经完全消除。
2. TSM Engine：底层采用自研的 TSM 存储引擎，TSM 也是基于 LSM 的思想，提供极强的写能力以及高压缩率，在后面的章节会对其做一个比较详细的分析。
3. InfluxQL：提供 SQL-Like 的查询语言，极大的方便了使用，数据库在易用性上演进的终极目标都是提供 Query Language。
4. Continuous Queries: 通过 CQ 能够支持 auto-rollup 和 pre-aggregation，对常见的查询操作可以通过 CQ 来预计算加速查询。
5. TimeSeries Index: 对 Tags 会进行索引，提供高效的检索。这一项功能，对比 OpenTSDB 和 KairosDB 等，在 Tags 检索的效率上提升了不少。OpenTSDB 在 Tags 检索上做了不少的查询优化，但是受限于 HBase 的功能和数据模型，所以然并卵。不过目前稳定版中的实现采用的是 memory-based index 的实现方式，这种方案在实现上比较简单，查询上效率最高，但是带来了不少的问题，在下面的章节会详细描述。
6. Plugin Support: 支持自定义插件，能够扩展到兼容多种协议，如 Graphite、collectd 和 OpenTSDB。

TSM

InfluxDB 底层的存储引擎经历了从 LevelDB 到 BlotDB，再到选择自研 TSM 的过程，整个选择转变的思考可以在其官网文档里看到。整个思考过程很值得借鉴，对技术选型和转变的思考总是比平白的描述某个产品特性让人印象深刻的多。

我简单总结下它的整个存储引擎选型转变的过程，第一阶段是 LevelDB，选型 LevelDB 的主要原因是其底层数据结构采用 LSM，对写入很友好，能够提供很高的写入吞吐量，比较符合时序数据的特性。在 LevelDB 内，数据是采用 KeyValue 的方式存储且按 Key 排序，InfluxDB 使用的 Key 设计是 SeriesKey+Timestamp 的组合，所以相同 SeriesKey 的数据是按 timestamp 来排序存储的，能够提供很高效的按时间范围的扫描。

不过使用 LevelDB 的一个最大的问题是，InfluxDB 支持历史数据自动删除（Retention Policy），在时序数据场景下数据自动删除通常是大块的连续时间段的历史数据删除。LevelDB 不支持 Range delete 也不支持 TTL，所以要删除只能是一个一个 key 的删除，会造成大量的删除流量压力，且在 LSM 这种数据结构下，真正的物理删除不是即时的，在 compaction 时才会生效。各类 TSDB 实现数据删除的做法大致分为两类：

1. 数据分区：按不同的时间范围划分为不同的分区（Shard），因为时序数据写入都是按时间线性产生的，所以分区的产生也是按时间线性增长的，写入通常是在最新的分区，而不会散列到多个分区。分区的优点是数据回收的物理删除非常简单，直接把整个分区删除即可。缺点是数据回收的精细度比较大，为整个分区，而回收的时间精度取决于分区的时间跨度。分区的实现可以是在应用层提供，也可以是存储引擎层提供，例如可以利用 RocksDB 的 column family 来作为数据分区。InfluxDB 采用这种模式，默认的 Retention Policy 下数据会以 7 天时间跨度组成为一个分区。
2. TTL：底层数据引擎直接提供数据自动过期的功能，可以为每条数据设定存储时间（time to live），当数据存活时间到达后存储引擎会自动对数据进行物理删除。这种方式的优点是数据回收的精细度很高，精细到秒级及行级的数据回收。缺点是 LSM 的实现上，物理删除发生在 compaction 的时候，比较不及时。RocksDB、HBase、Cassandra 和阿里云表格存储都提供数据 TTL 的功能。

InfluxDB 采用的是第一种策略，会按 7 天一个周期，将数据分为多个不同的 Shard，每个 Shard 都是一个独立的数据库实例。随着运行时间的增长，shard 的个数会越来越多。而由于每个 shard 都是一个独立的数据库实例，底层都是一套独立的 LevelDB 存储引擎，这时带来的问题是，每个存储引擎都会打开比较多的文件，随着 shard 的增多，最终进程打开的文件句柄会很快触及到上限。LevelDB 底层采用 level compaction 策略，是文件数多的原因之一。实际上 level compaction 策略不适合时序数据这种写入模式，这点原因 InfluxDB 没有提及。

由于遇到大量的客户反馈文件句柄过多的问题，InfluxDB 在新版本的存储引擎选型中选择了 BoltDB 替换 LevelDB。BoltDB 底层数据结构是 mmap B+树，其给出的选型理由是：1.与 LevelDB 相同语义的 API；2.纯 Go 实现，便于集成和跨平台；3.单个数据库只使用一个文件，解决了文件句柄消耗过多的问题，这条是他们选型 BoltDB 的最主要理由。但是 BoltDB 的 B+树结构与 LSM 相比，在写入能力上是一个弱势，B+树会产生大量的随机写。所以 InfluxDB 在使用 BoltDB 之后，很快遇到了 IOPS 的问题，当数据库大小达到几个 GB 后，会经常遇到 IOPS 的瓶颈，极大影响写入能力。虽然 InfluxDB 后续也采用了一些写入优化措施，例如在 BoltDB 之前加了一层 WAL，数据写入先写 WAL，WAL 能保证数据是顺序写盘，但是最终写入 BoltDB 还是会带来比较大的 IOPS 资源消耗。

InfluxDB 在经历了几个小版本的 BoltDB 后，最终决定自研 TSM，TSM 的设计目标一是解决 LevelDB 的文件句柄过多问题，二是解决 BoltDB 的写入性能问题。TSM 全称是 Time-Structured Merge Tree，思想类似 LSM，不过是基于时序数据的特性做了一些特殊的优化。来看下 TSM 的一些重要组件：

1. Write Ahead Log(WAL) : 数据会先写入 WAL，后进入 memory-index 和 cache，写入 WAL 会同步刷盘，保证数据持久化。Cache 内数据会异步刷入 TSM File，在 Cache 内数据未持久化到 TSM File 之前若遇到进程 crash，则会通过 WAL 内的数据来恢复 cache 内的数据，这个行为与 LSM 是完全类似的。
2. Cache: TSM 的 Cache 与 LSM 的 MemoryTable 类似，其内部的数据为 WAL 中未持久化到 TSM File 的数据。若进程发生 failover，则 cache 中的数据会根据 WAL 中的数据进行重建。Cache 内数据保存在一个 SortedMap 中，Map 的 Key 为 TimeSeries+Timestamp 的组成。所以可以看到，在内存中数据是按 TimeSeries 组织的，TimeSeries 中的数据按时间顺序存放。
3. TSM Files: TSM File 与 LSM 的 SSTable 类似，TSM File 由四个部分组成，分别为：header, blocks, index 和 footer。其中最重要的部分是 blocks 和 index：
   • Block：每个 block 内存储的是某个 TimeSeries 的一段时间范围内的值，即某个时间段下某个 measurement 的某组 tag set 对应的某个 field 的所有值，Block 内部会根据 field 的不同的值的类型采取不同的压缩策略，以达到最优的压缩效率。
   • Index：文件内的索引信息保存了每个 TimeSeries 下所有的数据 Block 的位置信息，索引数据按 TimeSeries 的 Key 的字典序排序。在内存中不会把完整的 index 数据加载进去，这样会很大，而是只对部分 Key 做索引，称之为 indirectIndex。indirectIndex 中会有一些辅助定位的信息，例如该文件中的最小最大时间以及最小最大 Key 等，最重要的是保存了部分 Key 以及其 Index 数据的文件 offset 信息。若想要定位某个 TimeSeries 的 Index 数据，会先根据内存中的部分 Key 信息找到与其最相近的 Index Offset，之后从该起点开始顺序扫描文件内容再精确定位到该 Key 的 Index 数据位置。

4. Compaction: compaction 是一个将 write-optimized 的数据存储格式优化为 read-optimized 的数据存储格式的一个过程，是 LSM 结构存储引擎做存储和查询优化很重要的一个功能，compaction 的策略和算法的优劣决定了存储引擎的质量。在时序数据的场景下，基本很少发生 update 或者 delete，数据都是按时间顺序生成的，所以基本不会有 overlap，Compaction 起到的作用主要在于压缩和索引优化。

   • LevelCompaction: InfluxDB 将 TSM 文件分为 4 个层级(Level 1-4)，compaction 只会发生在同层级文件内，同层级的文件 compaction 后会晋升到下一层级。从这个规则看，根据时序数据的产生特性，level 越高数据生成时间越旧，访问热度越低。由 Cache 数据初次生成的 TSM 文件称为 Snapshot，多个 Snapshot 文件 compaction 后产生 Level1 的 TSM 文件，Level1 的文件 compaction 后生成 level2 的文件，依次类推。低 Level 和高 Level 的 compaction 会采用不同的算法，低 level 文件的 compaction 采用低 CPU 消耗的做法，例如不会做解压缩和 block 合并，而高 level 文件的 compaction 则会做 block 解压缩以及 block 合并，以进一步提高压缩率。我理解这种设计是一种权衡，compaction 通常在后台工作，为了不影响实时的数据写入，对 compaction 消耗的资源是有严格的控制，资源受限的情况下必然会影响 compaction 的速度。而 level 越低的数据越新，热度也越高，需要有一种更快的加速查询的 compaction，所以 InfluxDB 在低 level 采用低资源消耗的 compaction 策略，这完全是贴合时序数据的写入和查询特性来设计的。
   • IndexOptimizationCompaction: 当 Level4 的文件积攒到一定个数后，index 会变得很大，查询效率会变的比较低。影响查询效率低的因素主要在于同一个 TimeSeries 数据会被多个 TSM 文件所包含，所以查询不可避免的需要跨多个文件进行数据整合。所以 IndexOptimizationCompaction 的主要作用就是将同一 TimeSeries 下的数据合并到同一个 TSM 文件中，尽量减少不同 TSM 文件间的 TimeSeries 重合度。
   • FullCompaction: InfluxDB 在判断某个 Shard 长时间内不会再有数据写入之后，会对数据做一次 FullCompaction。FullCompaction 是 LevelCompaction 和 IndexOptimization 的整合，在做完一次 FullCompaction 之后，这个 Shard 不会再做任何的 compaction，除非有新的数据写入或者删除发生。这个策略是对冷数据的一个规整，主要目的在于提高压缩率。

TimeSeries Index

时序数据库除了支撑时序数据的存储和计算外，还需要能够提供多维度查询。InfluxDB 为了提供更快速的多维查询，对 TimeSeries 进行了索引。关于数据和索引，InfluxDB 是这么描述自己的：

InfluxDB actually looks like two databases in one: a time series data store and an inverted index for the measurement, tag, and field metadata.

在 InfluxDB 1.3 之前，TimeSeries Index(下面简称为 TSI)只支持 Memory-based 的方式，即所有的 TimeSeries 的索引都是放在内存内，这种方式有好处但是也会带来很多的问题。而在最新发布的 InfluxDB 1.3 版本上，提供了另外一种方式的索引可供选择，新的索引方式会把索引存储在磁盘上，效率上相比内存索引差一点，但是解决了内存索引存在的不少问题。

Memory-based Index

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

// Measurement represents a collection of time series in a database. It also
    // contains in memory structures for indexing tags. Exported functions are
    // goroutine safe while un-exported functions assume the caller will use the
    // appropriate locks.
    type Measurement struct {
     database string
     Name     string `json:"name,omitempty"`
     name     []byte // cached version as []byte

     mu         sync.RWMutex
     fieldNames map[string]struct{}

     // in-memory index fields
     seriesByID          map[uint64]*Series              // lookup table for series by their id
     seriesByTagKeyValue map[string]map[string]SeriesIDs // map from tag key to value to sorted set of series ids

     // lazyily created sorted series IDs
     sortedSeriesIDs SeriesIDs // sorted list of series IDs in this measurement
    }

    // Series belong to a Measurement and represent unique time series in a database.
    type Series struct {
     mu          sync.RWMutex
     Key         string
     tags        models.Tags
     ID          uint64
     measurement *Measurement
     shardIDs    map[uint64]struct{} // shards that have this series defined
    }

如上是 InfluxDB 1.3 的源码中对内存索引数据结构的定义，主要有两个重要的数据结构体：

Series: 对应某个 TimeSeries，其内存储 TimeSeries 相关的一些基本属性以及它所属的 Shard

• Key：对应 measurement + tags 序列化后的字符串。
• tags: 该 TimeSeries 下所有的 TagKey 和 TagValue
• ID: 用于唯一区分的整数 ID。
• measurement: 所属的 measurement。
• shardIDs: 所有包含该 Series 的 ShardID 列表。

Measurement: 每个 measurement 在内存中都会对应一个 Measurement 结构，其内部主要是一些索引来加速查询。

• seriesByID：通过 SeriesID 查询 Series 的一个 Map。
• seriesByTagKeyValue：双层 Map，第一层是 TagKey 对应其所有的 TagValue，第二层是 TagValue 对应的所有 Series 的 ID。可以看到，当 TimeSeries 的基数变得很大，这个 map 所占的内存会相当多。
• sortedSeriesIDs：一个排序的 SeriesID 列表。

全内存索引结构带来的好处是能够提供非常高效的多维查询，但是相应的也会存在一些问题：

• 能够支持的 TimeSeries 基数有限，主要受限于内存的大小。若 TimeSeries 个数超过上限，则整个数据库会处于不可服务的状态。这类问题一般由用户错误的设计 TagKey 引发，例如某个 TagKey 是一个随机的 ID。一旦遇到这个问题的话，也很难恢复，往往只能通过手动删数据。
• 若进程重启，恢复数据的时间会比较长，因为需要从所有的 TSM 文件中加载全量的 TimeSeries 信息来在内存中构建索引。

Disk-based Index

针对全内存索引存在的这些问题，InfluxDB 在最新的 1.3 版本中提供了另外一种索引的实现。得益于代码设计上良好的扩展性，索引模块和存储引擎模块都是插件化的，用户可以在配置中自由选择使用哪种索引。

InfluxDB 实现了一个特殊的存储引擎来做索引数据的存储，其结构也与 LSM 类似，如上图就是一个 Disk-based Index 的结构图，详细的说明可以参见设计文档。
索引数据会先写入 Write-Ahead-Log，WAL 中的数据按 LogEntry 组织，每个 LogEntry 对应一个 TimeSeries，包含 Measurement、Tags 以及 checksum 信息。写入 WAL 成功后，数据会进入一个内存索引结构内。当 WAL 积攒到一定大小后，LogFile 会 Flush 成 IndexFile。IndexFile 的逻辑结构与内存索引的结构一致，表示的也是 Measurement 到 TagKey，TagKey 到 TagValue，TagValue 到 TimeSeries 的 Map 结构。InfluxDB 会使用 mmap 来访问文件，同时文件中对每个 Map 都会保存 HashIndex 来加速查询。

当 IndexFile 积攒到一定数量后，InfluxDB 也提供 compaction 的机制，将多个 IndexFile 合并为一个，节省存储空间以及加速查询。

简介

由于桂电实验室上网需要 高额的 费用，考虑到实验室和宿舍的网络都是基于校园网来进行内网连接的，基于这一点，考虑在宿舍通过笔记本或树莓派设备来启动一个vpn服务器连接内网，然后再在宿舍的设备上将内外网进行桥接，即该设备可以同时上内外网，由于大多数笔记本或者树莓派都具有双网卡，所以采用无线网卡来接入一个已经具备上网功能的路由器，使用有线网卡连接内网。

2016-12-15 update
最近又被2.4g网络恶心到了，宿舍那边的无线信号真的是太多了，各种信道拥堵，而英产树莓派又不支持伟大的13信道和大陆5g频段，所以ping一直都有波动，考虑买大陆的usb无线网卡或有线网卡来接入5g网络或者有线网路提高树莓派外网连接的稳定性，当然宿舍不缺电(桂电宿舍普通用电还要自己交钱,无力吐槽)准备使用笔记本搭建的童鞋当我没说，因为新一点的笔记本都支持5g吧….

配置 永不掉线 的路由器

桂电宿舍的网线都是单网线三网通用的，其实原理很简单，就是在上层做了一下网关开放的工作，通过一个叫做出校器的工具，选择一个运营商，将拨号所用的mac地址和相关的运营商进行绑定，此后的所有的数据包都发往指定运营商的网关，基于这个原理，可以在实验室等能够连通内网的设备上定期进行相关端口开放的工作(前提是将该设备的mac修改为路由器的mac地址)，另外，这里推荐一个师大师兄编写的mac、linux、windows下的第三方出校器和端口开放工具ipclient_gxnu,项目中的有详细的介绍和文档，推荐学习。此外，如果仅仅是需要进行运营商和mac地址的绑定的话，推荐使用桂电某学生编写的在线端口绑定网站:http://sec.guet.edu.cn/open/将路由mac地址和某运营商端口进行绑定

ubuntu发行版本选择

由于之前我用的是ubuntu的最新的发行版本，在dhcp的时候经常会出现三个默认路由的情况，我也没有深入研究原因，后来换到16.04LTS上后，同样的配置，dhcp后默认只有一个默认路由，所以推荐16.04LTS

配置

安装pptpd

1

sudo apt-get install pptpd

配置虚拟ip，编辑/etc/pptpd.conf ( 这一步可以不用做，因为python脚本中会覆盖 ):

1
2

localip 10.20.39.111 # 本机ip
remoteip 10.100.123.2-100 # 分配的ip段

在/etc/ppp/pptpd-options下中设置dns:

1
2
3

#根据实际情况设置dns
ms-dns 192.168.199.1
ms-dns 114.114.114.114

在/etc/ppp/chap-secrets中配置vpn账号:

1

"user"  pptpd   "user"  * #星号是不限制ip的意思

不过默认情况下，pptpd无法给vpn连接分配ip，所以如果是多用户的话需要手动分配ip具体配置类似:

1
2

"user1"   pptpd   "user1"   10.100.123.2
"user2"   pptpd   "user2"   10.100.123.3

重启pptpd服务:

1

sudo /etc/init.d/pptpd restart

在/etc/sysctl.conf中配置ip转发(取消该行注释):

1

net.ipv4.ip_forward=1

使配置立即生效:

1

sudo sysctl -p

安装iptables,这个是用于配置NAT映射的:

1

sudo apt-get install iptables

建立一个外网NAT（外网走无线）:

1

sudo iptables -t nat -A POSTROUTING -s 10.100.123.0/24 -o wlo1 -j MASQUERADE

建立一个内网NAT（内网走有线）:

1

sudo iptables -t nat -A POSTROUTING -s 10.100.123.0/24 -d 172.16.0.0/16 -o eno1 -j MASQUERADE

其中-o参数配置的是流量的出口,也就是我这的外网出口
设置MTU,防止包过大而丢包:

1

sudo iptables -A FORWARD -s 10.100.123.0/24 -p tcp -m tcp --tcp-flags SYN,RST SYN -j TCPMSS --set-mss 1200

保存规则(此处需要root权限):

1

sudo iptables-save >/etc/iptables-rules

编辑/etc/network/interfaces,在末尾加一行,使网卡加载时自动加载规则:

1

per-up iptables-restore </etc/iptables-rules

配置到此为止

网卡名称修改问题

新版的ubuntu网卡名称都是随机的，可以自定义修改网卡的名称，比如本文章中，有线网卡为:wlo1， 无线网卡为:eno1。
默认，/etc/udev/rules.d/只有一个README文件。
新建了70-persistent-net.rules文件，然后编辑：

1

SUBSYSTEM=="net", ACTION=="add", ATTR{address}=="44:33:4c:07:ad:48", NAME="eno1"

服务器启动代码

目的

1. 修改dhcp后的ip为静态ip
2. 添加内外网路由，默认情况下重启后路由表会丢失
3. 持续ping对方网关，保证服务器的稳定，推荐使用tmux来维持会话状态，保证程序存活

启动方式

安装 nodejs 和 npm :

1

sudo apt install nodejs npm

切换到 /usr/bin 目录下，建立一个 node 到 nodejs 的软连接，因为 pm2 启动时需要执行 node 命令:

1
2

cd /usr/bin
sudo ln -s ./node.js node

使用 npm 安装 pm2 :

1

sudo npm install -g pm2

使用 pm2 启动项目，并将其加入开启自启中:

1
2
3
4

cd vpn_launch
pm2 start ./launch.py --name="vpn"
pm2 save
pm2 startup

至此，您的pc、树莓派已经具有了开机自启、daemon、线路自检等功能，理论上已经不会掉线
代码地址:leftjs/vpn_launch

launch.py:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import socket, fcntl, struct
import commands
import time
import smtplib
from email.mime.text import MIMEText
from email.header import Header

# 第三方 SMTP 服务
mail_host="smtp.qq.com"  #设置服务器
mail_user="leftjs@foxmail.com"    #用户名
mail_pass="xxxx"   #授权口令
sender = 'leftjs@foxmail.com'
receivers = ['lefttjs@gmail.com']  # 接收邮件，可设置为你的QQ邮箱或者其他邮箱



def send_email(text):
    message = MIMEText('%s' % text, 'plain', 'utf-8')
    message['From'] = Header("leftjs", 'utf-8')
    message['To'] =  Header("jason zhang", 'utf-8')
    subject = 'vpn 报告'
    message['Subject'] = Header(subject, 'utf-8')
    try:
        smtpObj = smtplib.SMTP_SSL()
        smtpObj.connect(mail_host, 465)    # 25 为 SMTP 端口号
        smtpObj.login(mail_user,mail_pass)
        smtpObj.sendmail(sender, receivers, message.as_string())
        print "邮件发送成功"
    except smtplib.SMTPException:
        print "Error: 无法发送邮件"

def get_local_ip(ifname):
    try:
        s = socket.socket(socket.AF_INET, socket.SOCK_DGRAM)
        inet = fcntl.ioctl(s.fileno(), 0x8915, struct.pack('256s', ifname[:15]))
        return socket.inet_ntoa(inet[20:24])
    except Exception, e:
        send_email(str(e))
        return

def check_ping():
    (ping_state, res) = commands.getstatusoutput('ping 202.193.75.254 -c 2')
    # (ping_state_baidu, res_baidu) = commands.getstatusoutput('ping www.baidu.com -c 2')
    # ping_state == 0 when ping is ok
    # return True if ping_state == 0 and ping_state_baidu == 0 else False
    return True if ping_state == 0 else False

def read_file_content(file_name):
    the_file = open(file_name, 'r')
    file_content = the_file.read()
    the_file.close()
    return file_content

def write_file_content(file_name, new_content):
    out_file = open(file_name, 'w')
    out_file.write(new_content)
    out_file.close()

def create_interfaces_static_file(intranet_ip):
    raw_content = read_file_content('./interfaces/raw_interfaces_static')
    write_file_content('./interfaces/interfaces_static', raw_content % intranet_ip)

def restart_pptpd(intranet_ip):
    raw_content = read_file_content('./pptpd/raw_pptpd.conf')
    write_file_content('./pptpd/pptpd.conf', raw_content % intranet_ip)
    commands.getstatusoutput('cp -f ./pptpd/pptpd.conf /etc/pptpd.conf')
    commands.getstatusoutput('sudo /etc/init.d/pptpd restart')

def restart_dnsmasq(intranet_ip):
    raw_content = read_file_content('./dns/raw_dnsmasq.conf')
    write_file_content('./dns/dnsmasq.conf', raw_content % intranet_ip)
    commands.getstatusoutput('cp -f ./dns/dnsmasq.conf /etc/dnsmasq.conf')
    commands.getstatusoutput('service dnsmasq restart')

def add_route_item():
    commands.getstatusoutput('ip route add 202.193.0.0/16 via 10.20.40.254 dev eno1')
    commands.getstatusoutput('ip route add 10.100.123.0/24 via 10.20.40.254 dev eno1')
    commands.getstatusoutput('ip route add 10.20.0.0/16 via 10.20.40.254 dev eno1')
    commands.getstatusoutput('ip route add 172.16.0.0/16 via 10.20.40.254 dev eno1')


if __name__ == '__main__':
    old_ip = None
    while True:
        ping_state = check_ping()
        if ping_state == False or old_ip == None:
            print time.strftime('%Y-%m-%d %H:%M:%S',time.localtime(time.time()))
            print 'network restart.'
            commands.getstatusoutput('dhclient eno1')
            # get new intranet ip
            intranet_ip = get_local_ip("eno1")
            if intranet_ip is None:
                continue
            if old_ip == None or old_ip != intranet_ip:
                print 'new ip: ',intranet_ip
                send_email('新的ip为: %s' % intranet_ip)
                create_interfaces_static_file(intranet_ip)
                restart_pptpd(intranet_ip)
                # restart_dnsmasq(intranet_ip)
                old_ip = intranet_ip
            commands.getstatusoutput('cp -f ./interfaces/interfaces_static /etc/network/interfaces')
            commands.getstatusoutput('/etc/init.d/networking restart')
            # commands.getstatusoutput('dhclient eth0')
            # commands.getstatusoutput('cp -f ./dns/resolv.conf /etc/resolv.dnsmasq.conf')
            add_route_item()
            time.sleep(1)
            print 'config complete.'
            continue
        time.sleep(2)

寝室ip扫描代码

在实验室连入校内网批量ping宿舍ip，找出自己的主机。

ping_test.py:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

from threading import Thread
import subprocess
from Queue import Queue

num_threads = 100
queue = Queue()
ips = ['10.20.38.' + str(a) for a in range(1, 255)] + ['10.20.39.' + str(a) for a in range(1, 255)]

#wraps system ping command
def pinger(i, q):
    """Pings subnet"""
    while True:
        ip = q.get()
        print "Thread %s: Pinging %s" % (i, ip)
        ret = subprocess.call("ping -c 1 %s" % ip,
            shell=True,
            stdout=open('/dev/null', 'w'),
            stderr=subprocess.STDOUT)
        if ret == 0:
            print "%s: is alive" % ip
            with open('./result.txt', 'a') as f:
                f.write("%s: is alive\n" % ip)
        else:
            print "%s: did not respond" % ip
        q.task_done()
#Spawn thread pool
for i in range(num_threads):
    worker = Thread(target=pinger, args=(i, queue))
    worker.setDaemon(True)
    worker.start()
#Place work in queue
for ip in ips:
    queue.put(ip)
#Wait until worker threads are done to exit
queue.join()